QUESTION: 1

An induction clutch works by __________.

magnetism
pneumatics
hydraulics
friction

Answer(s): A

Explanation:

An induction clutch is a magnetic clutch.

Reveal Solution Next Question

QUESTION: 2

If a first class lever with a resistance arm measuring 2 feet and an effort arm measuring 8 feet are being used, what’s the mechanical advantage?

Answer(s): B

Explanation:

Mechanical advantage can be calculated as Length of Effort Arm ÷ Length of Resistance Arm. MA = 8 ÷ 2 = 4.

Reveal Solution Next Question

The bottoms of four boxes are shown above. The boxes all have the same volume.
If postal regulations state that the sides of a box must meet a minimum height, which box is most likely to be too short to go through the mail?

NO. 4
NO. 2
NO. 1
NO. 3

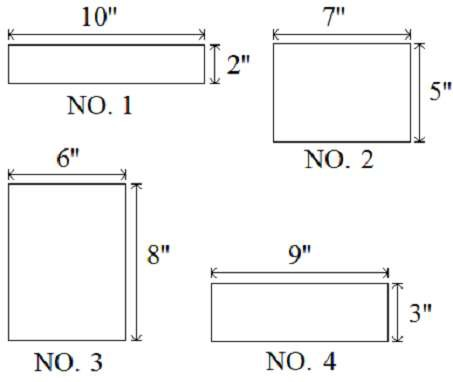
Answer(s): D

Explanation:

The box with the largest area on the bottom will have the shortest sides.
If length × width × height = volume, and all the boxes have equal volume, then the sides must be shortest on the box with the largest area on the bottom.
Calculate the area of each box bottom:
NO. 1 = 20 square inches;
NO. 2 = 35 square inches; NO. 3 = 48 square inches; and NO. 4 = 27 square inches.
NO. 3, which has the largest area, will have the shortest sides.

Reveal Solution Next Question